13  Working with distribution functions

Author

Affiliation

Sean Davis

University of Colorado
Anschutz School of Medicine

Which values do pnorm, dnorm, qnorm, and rnorm return? How do I remember the difference between these?

I find it helpful to have visual representations of distributions as pictures. It is difficult for me to think of distributions, or differences between probability, density, and quantiles without visualizing the shape of the distribution. So I figured it would be helpful to have a visual guide to pnorm, dnorm, qnorm, and rnorm.

Table 1.1: Functions for the normal distribution

Function	Input	Output
pnorm	x	P(X < x)
dnorm	x	f(x), or the height of the density curve at x
qnorm	q, a quantile from 0 to 1	x such that P(X < x) = q
rnorm	n	n random samples from the distribution

13.1 pnorm

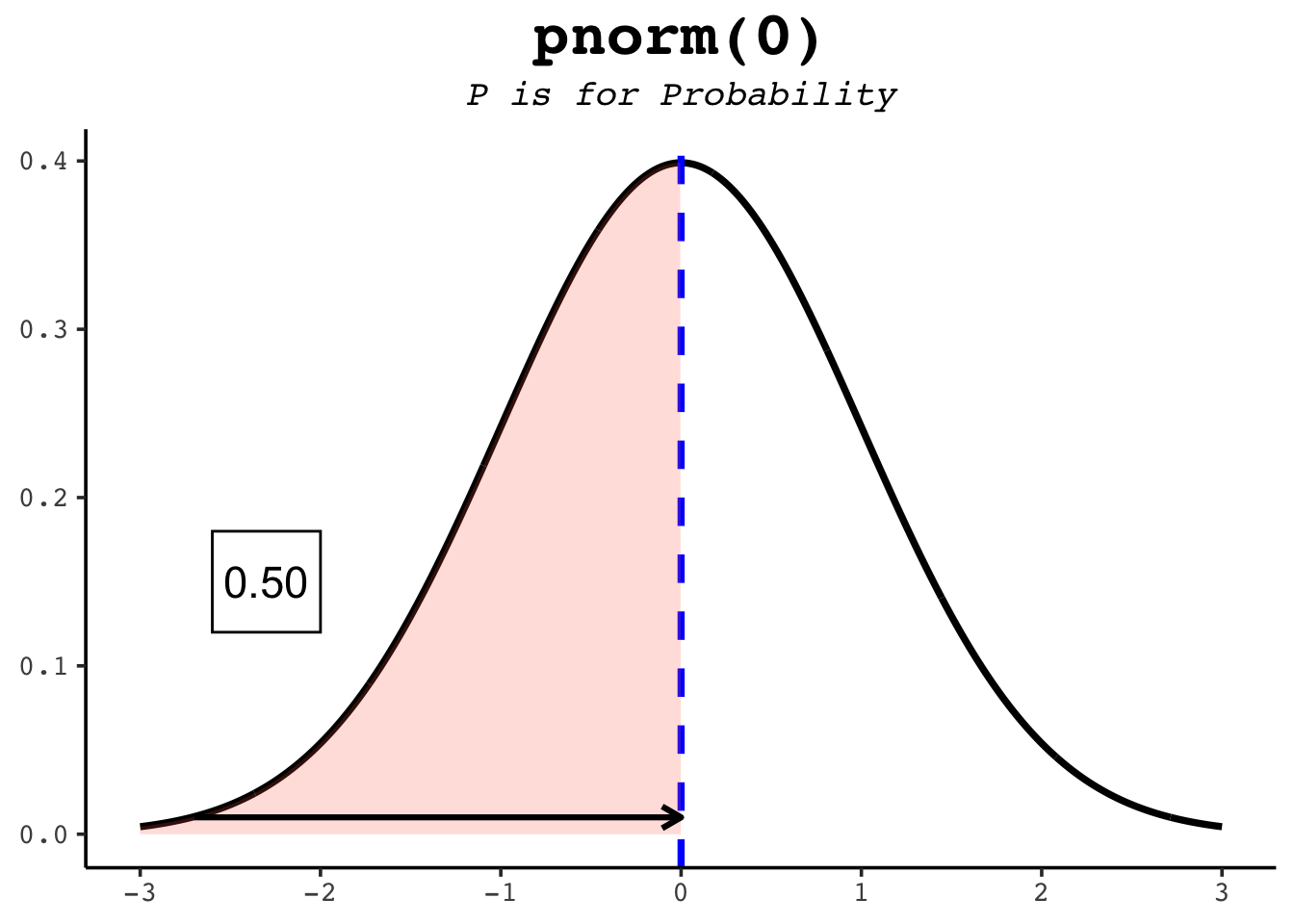
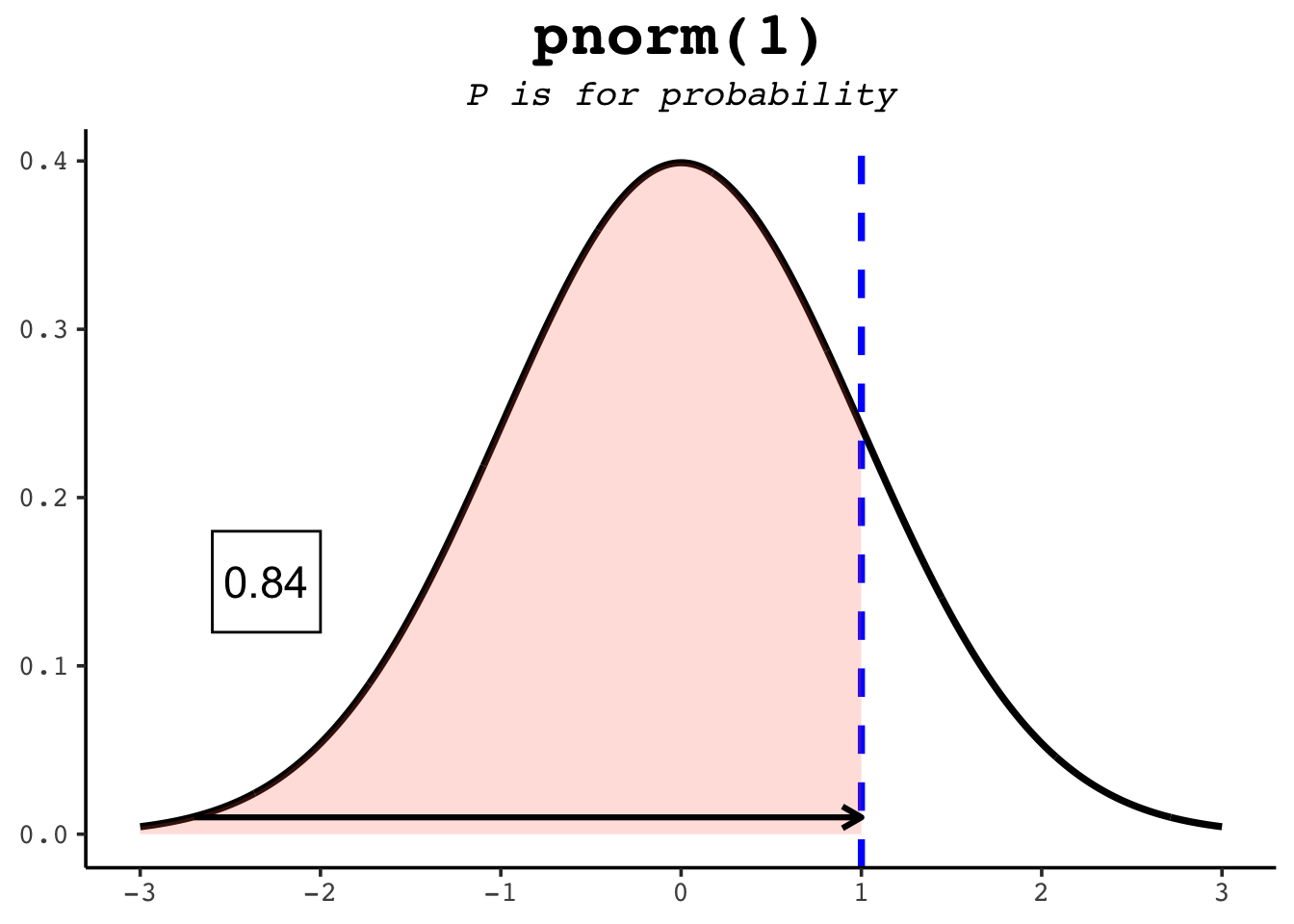
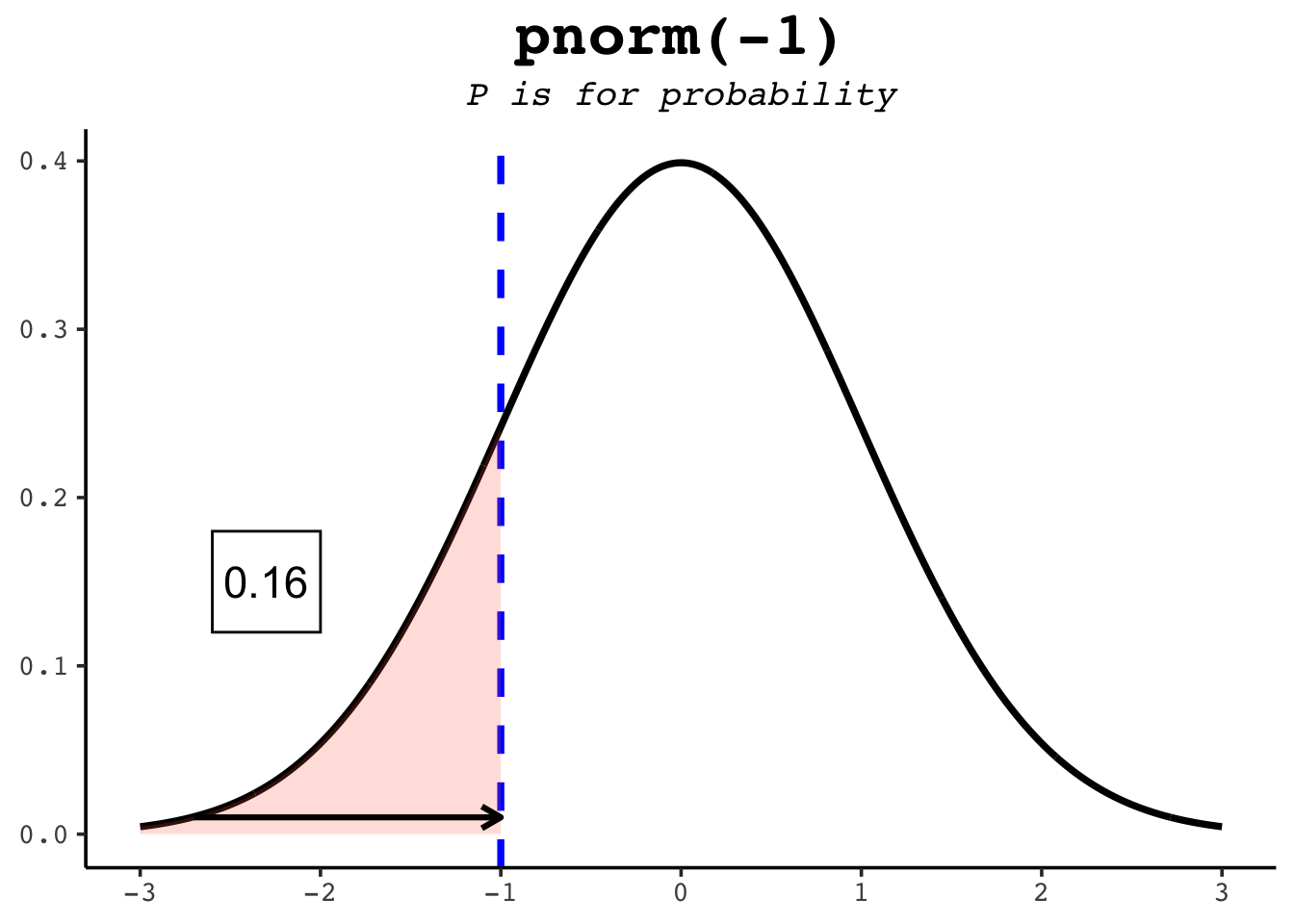
This function gives the probability function for a normal distribution. If you do not specify the mean and standard deviation, R defaults to standard normal. Figure 13.1

pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)

The R help file for pnorm provides the template above. The value you input for q is a value on the x-axis, and the returned value is the area under the distribution curve to the left of that point.

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

This function gives the probability function for a normal distribution. If you do not specify the mean and standard deviation, R defaults to standard normal.

pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) The R help file for pnorm provides the template above. The value you input for q is a value on the x-axis, and the returned value is the area under the distribution curve to the left of that point.

The option lower.tail = TRUE tells R to use the area to the left of the given point. This is the default, so will remain true even without entering it. In order to compute the area to the right of the given point, you can either switch to lower.tail = FALSE, or simply calculate 1-pnorm() instead. This is demonstrated below.

Figure 13.1: The pnorm function takes a quantile (value on the x-axis) and returns the area under the curve to the left of that value.

Figure 13.2: The pnorm function takes a quantile (value on the x-axis) and returns the area under the curve to the left of that value.

Figure 13.3: The pnorm function takes a quantile (value on the x-axis) and returns the area under the curve to the left of that value.

Figure 13.4: The pnorm function takes a quantile (value on the x-axis) and returns the area under the curve to the left of that value.

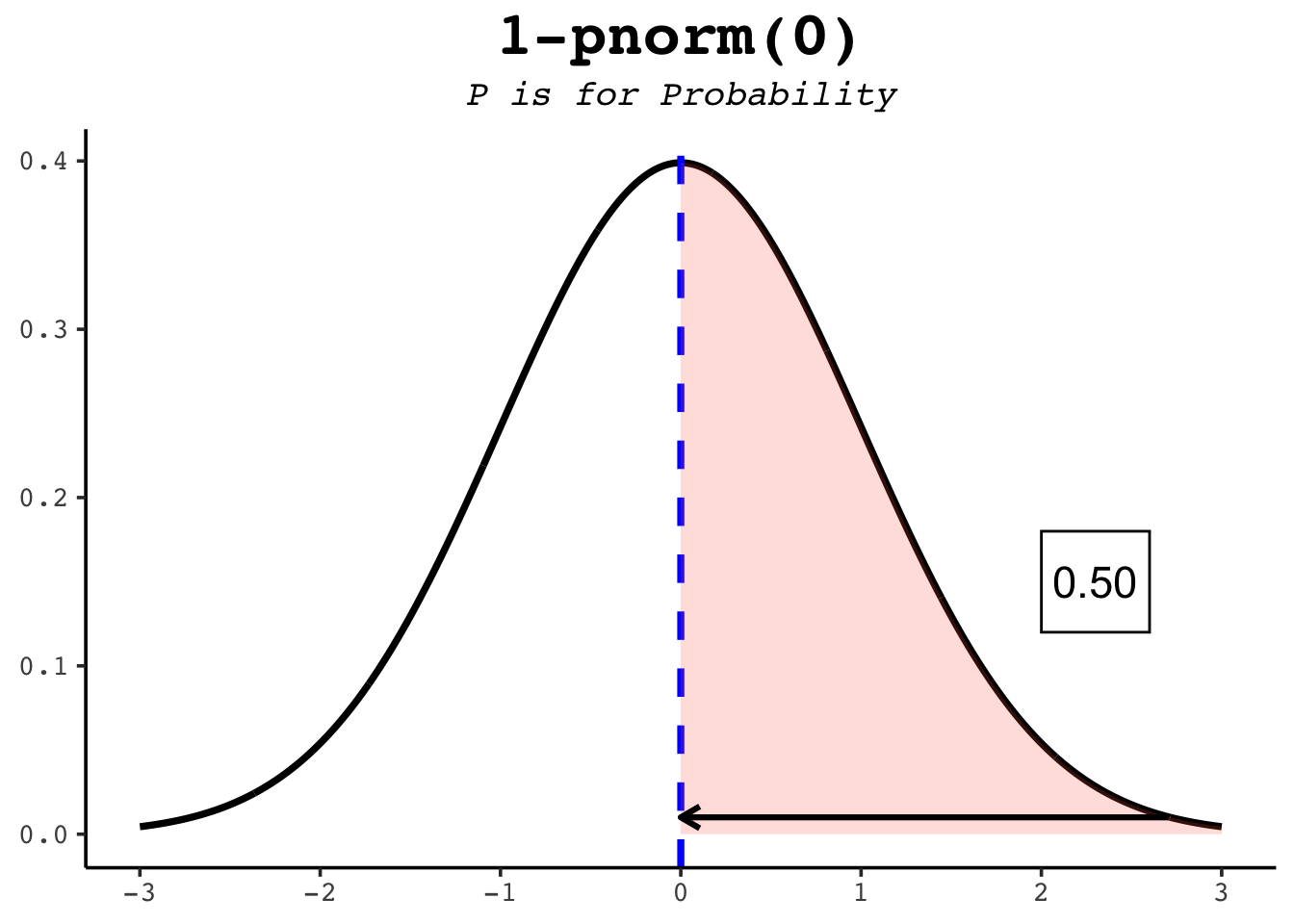
The option lower.tail = TRUE tells R to use the area to the left of the given point. This is the default, so will remain true even without entering it. In order to compute the area to the right of the given point, you can either switch to lower.tail = FALSE, or simply calculate 1-pnorm() instead.

13.2 dnorm

This function calculates the probability density function (PDF) for the normal distribution. It gives the probability density (height of the curve) at a specified value (x).

Figure 13.5: The dnorm function returns the height of the normal distribution at a given point.

Figure 13.6: The dnorm function returns the height of the normal distribution at a given point.

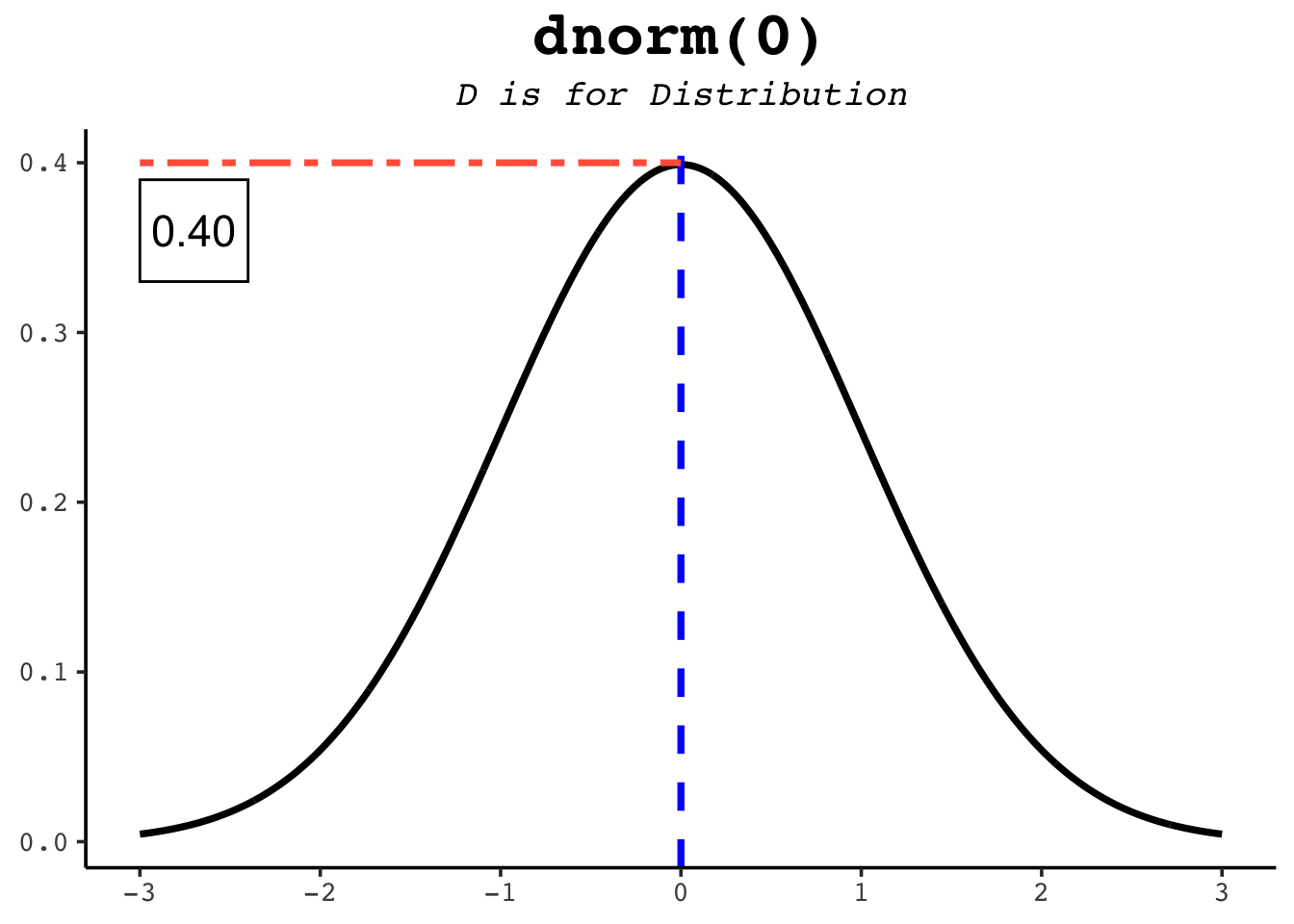
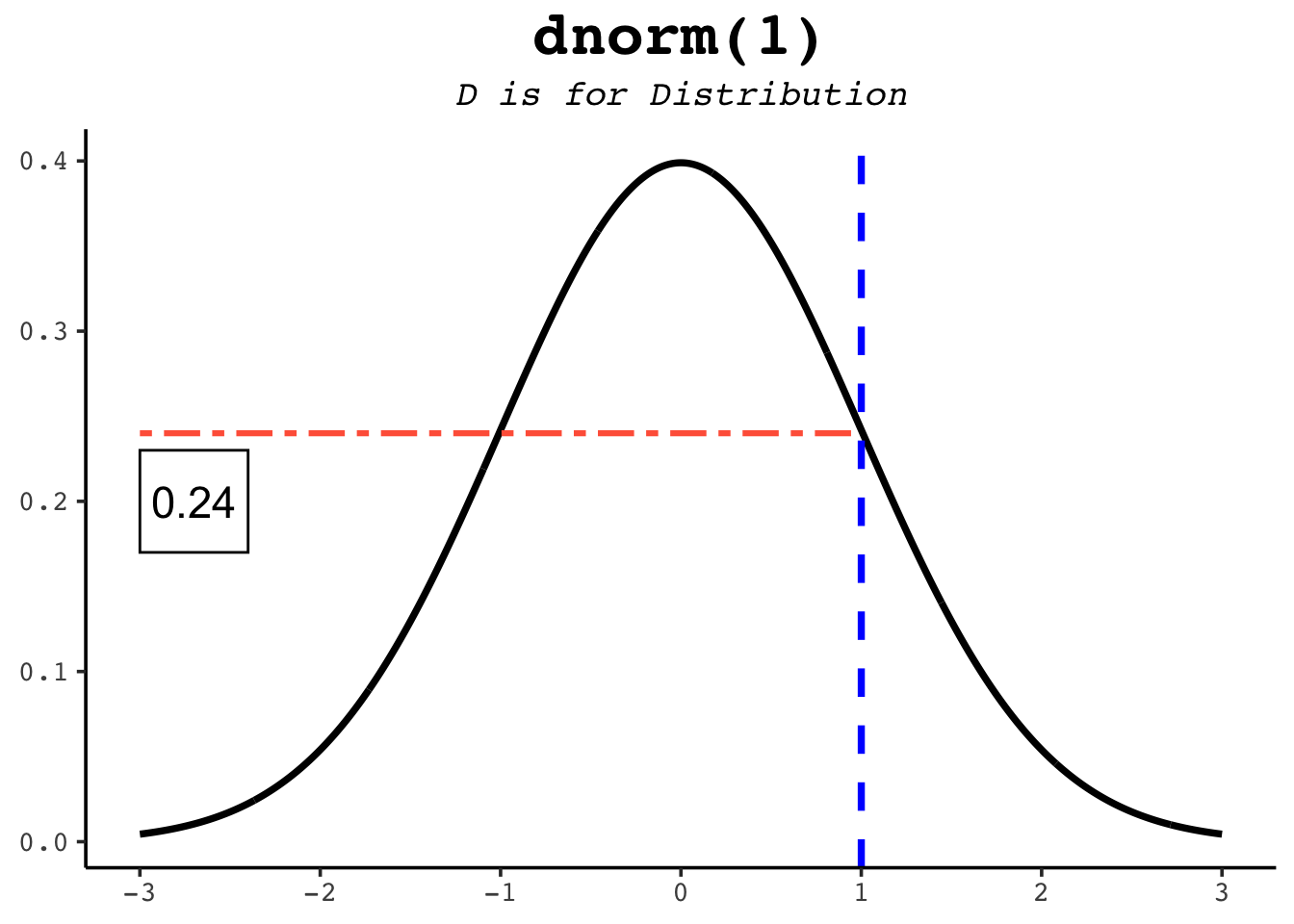
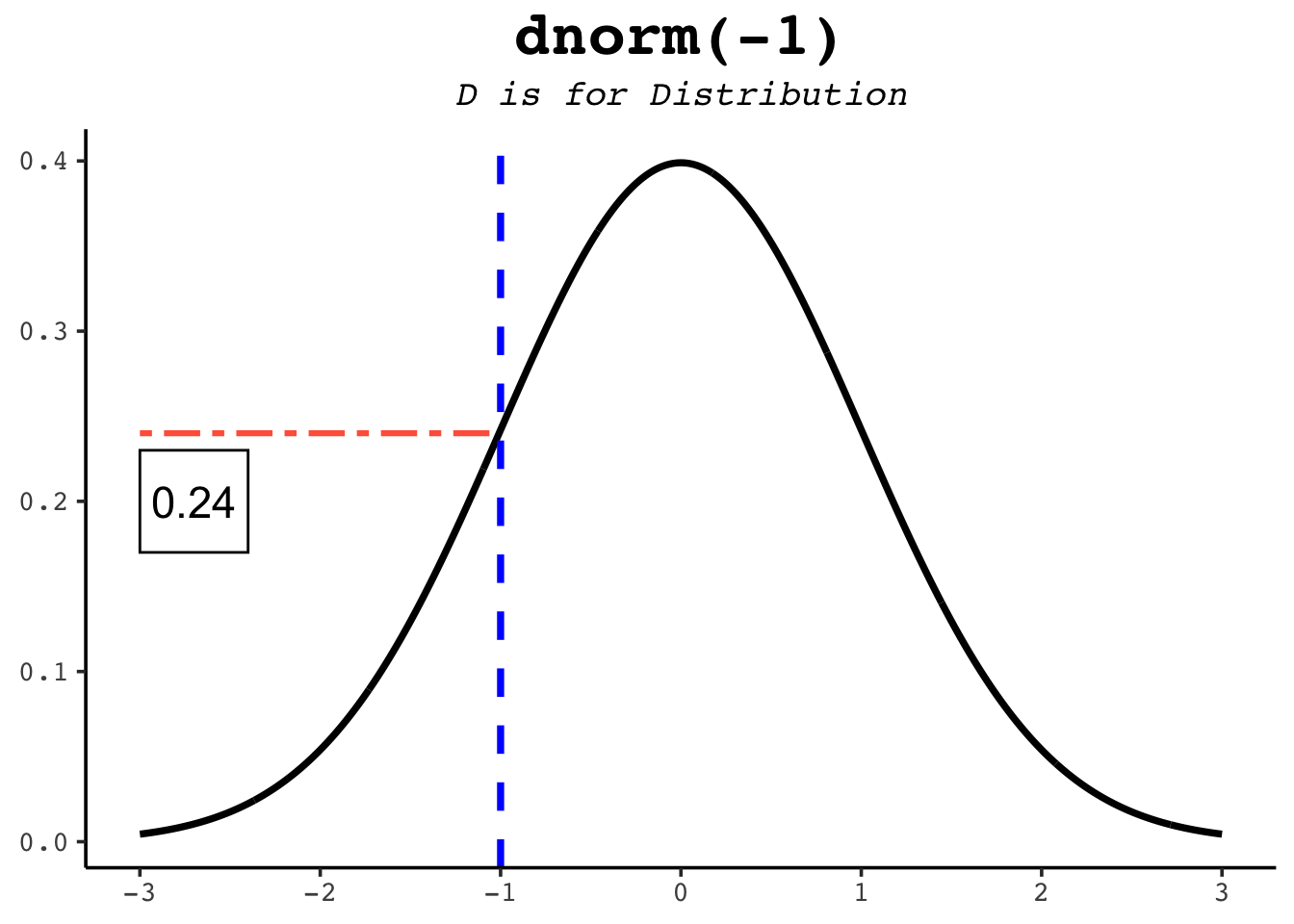
Figure 13.7: The dnorm function returns the height of the normal distribution at a given point.

13.3 qnorm

This function calculates the quantiles of the normal distribution. It returns the value (x) corresponding to a specified probability (p). It is the inverse of thepnorm function.

Figure 13.8: The qnorm function is the inverse of the pnorm function in that it takes a probability and gives the quantile.

Figure 13.9: The qnorm function is the inverse of the pnorm function in that it takes a probability and gives the quantile.

Figure 13.10: The qnorm function is the inverse of the pnorm function in that it takes a probability and gives the quantile.

Figure 13.11: The qnorm function is the inverse of the pnorm function in that it takes a probability and gives the quantile.

Figure 13.12: The qnorm function is the inverse of the pnorm function in that it takes a probability and gives the quantile.

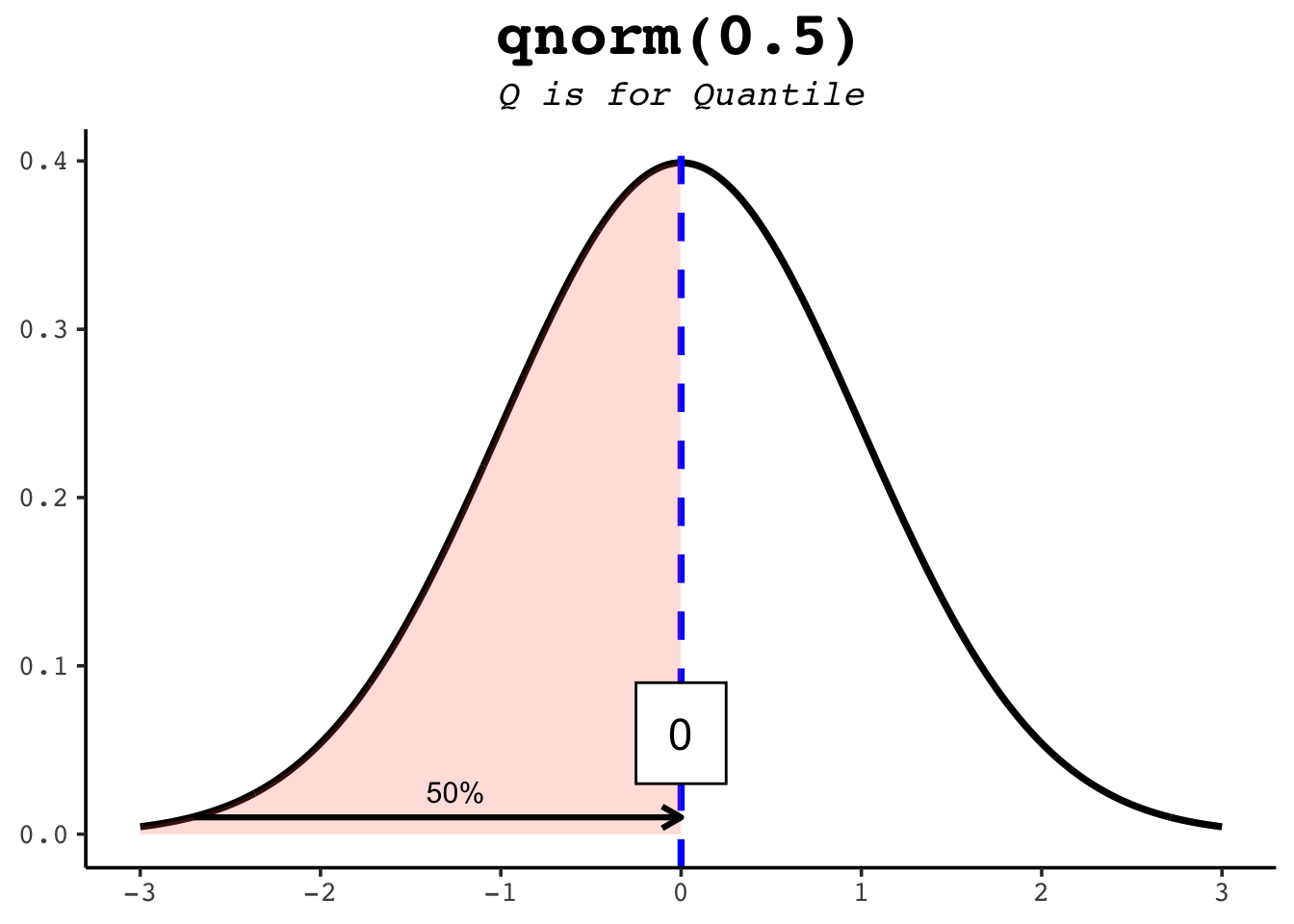
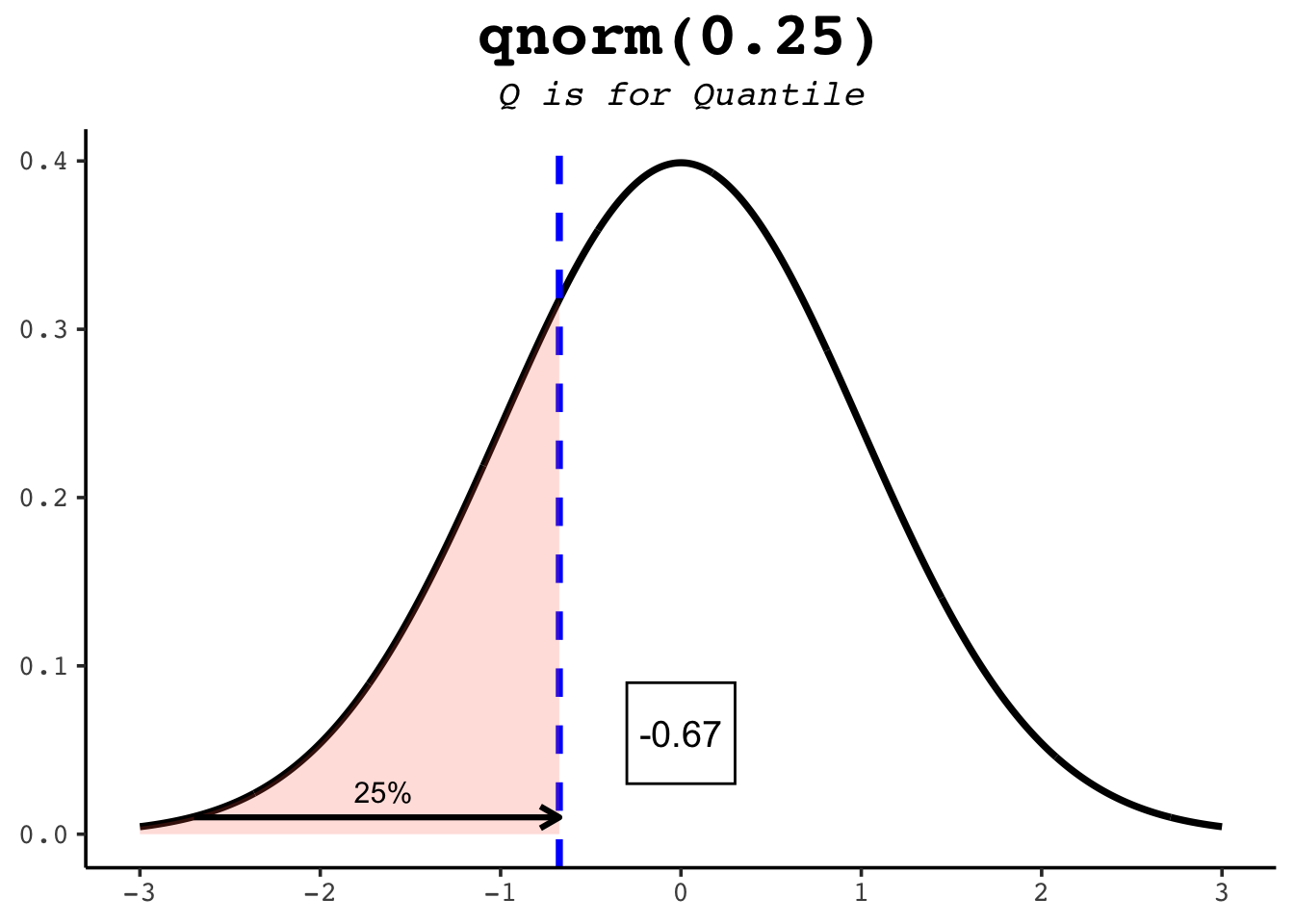
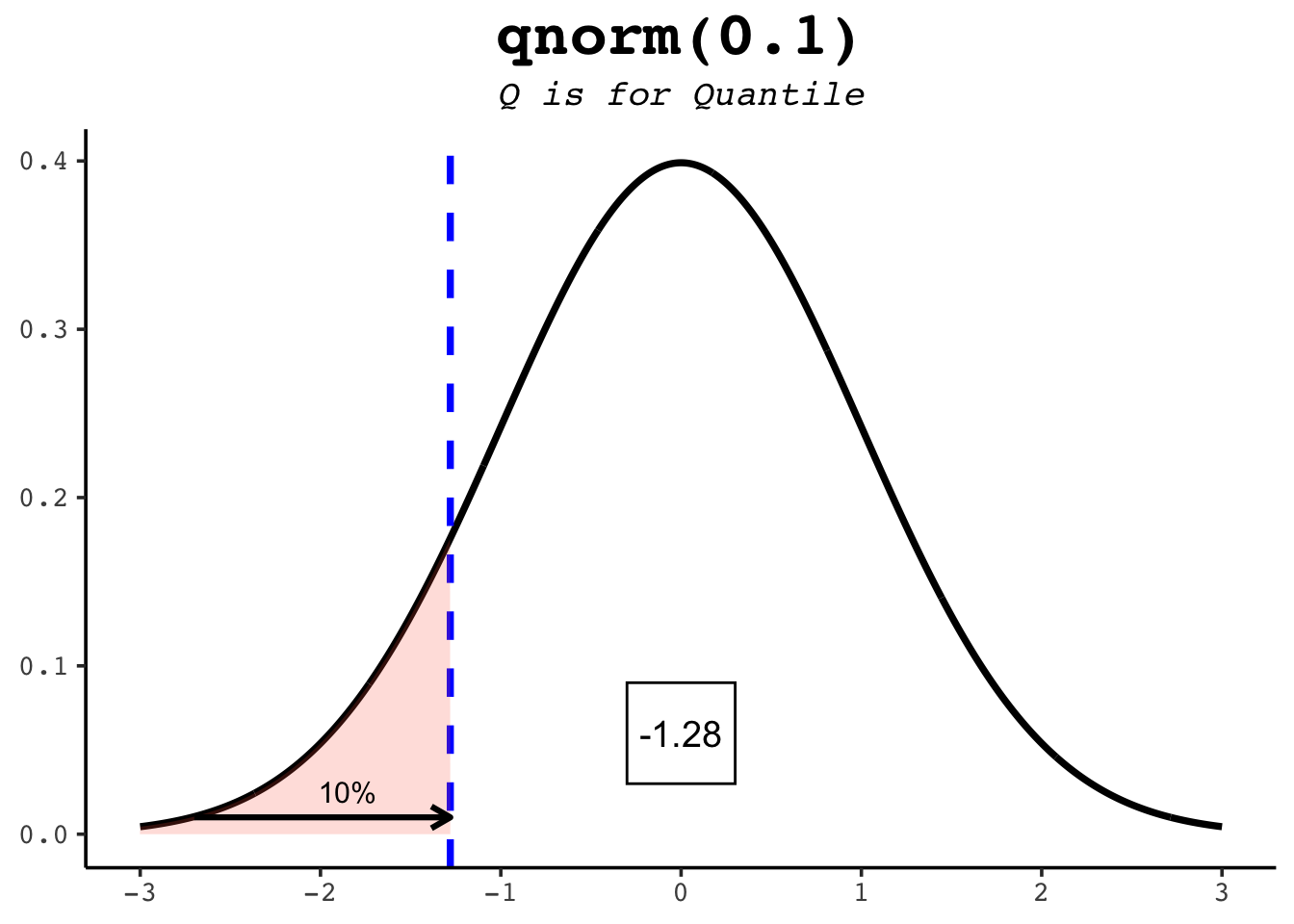
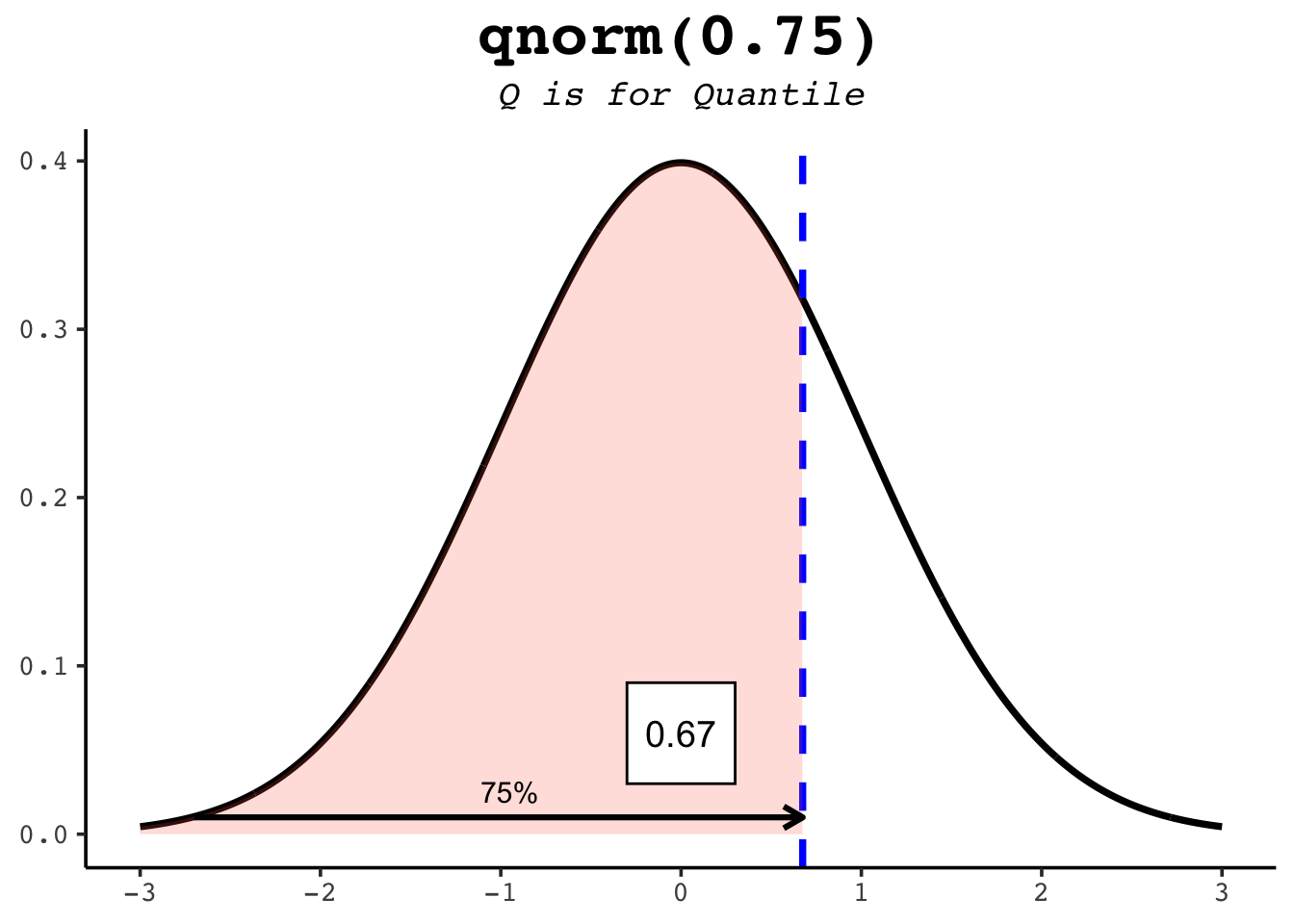
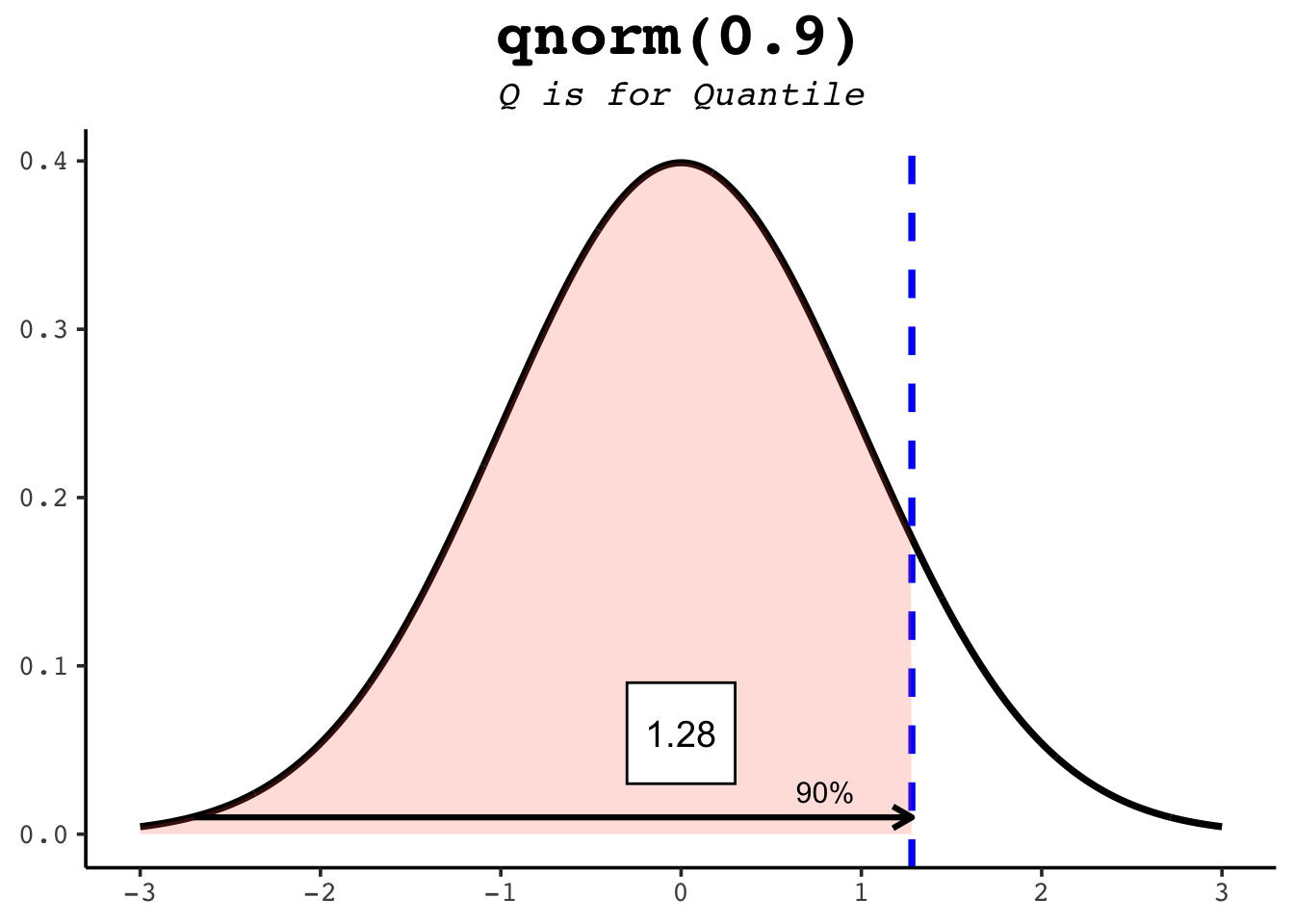
13.4 rnorm

print(r1)

Figure 13.13: The rnorm function takes a number of samples and returns a vector of random numbers from the normal distribution (with mean=0, sd=1 as defaults)

13.5 IQ scores

Normal Distribution and its Application with IQ

The normal distribution, also known as the Gaussian distribution, is a continuous probability distribution characterized by its bell-shaped curve. It is defined by two parameters: the mean (µ) and the standard deviation (σ). The mean represents the central tendency of the distribution, while the standard deviation represents the dispersion or spread of the data.

The IQ scores are an excellent example of the normal distribution, as they are designed to follow this distribution pattern. The mean IQ score is set at 100, and the standard deviation is set at 15. This means that the majority of the population (about 68%) have an IQ score between 85 and 115, while 95% of the population have an IQ score between 70 and 130.

• What is the probability of having an IQ score between 85 and 115?

  pnorm(115, mean = 100, sd = 15) - pnorm(85, mean = 100, sd = 15)

• What is the 90th percentile of the IQ scores?

  qnorm(0.9, mean = 100, sd = 15)

• What is the probability of having an IQ score above 130?

  1 - pnorm(130, mean = 100, sd = 15)

• What is the probability of having an IQ score below 70?

  pnorm(70, mean = 100, sd = 15)