20 Supervised Learning
In the previous chapter, we introduced the three main paradigms of machine learning: supervised, unsupervised, and reinforcement learning. We also highlighted the importance of a structured workflow, particularly the critical step of data splitting to prevent overfitting. Now, we’ll dive deeper into the world of supervised learning, the most common and widely applied category of machine learning.
This chapter provides a practical framework for understanding how different supervised learning algorithms work. Instead of viewing each algorithm as a completely separate entity, we’ll see that they all share a common conceptual structure. By grasping this structure, you can more easily understand, compare, and select the right algorithm for your problem. We will then use this framework to explore some of the most fundamental and popular algorithms for both regression and classification tasks.
20.1 A Framework for Understanding Supervised Algorithms
At a high level, every supervised learning algorithm can be understood as having three core components: the hypothesis space, the objective function, and the learning algorithm. Thinking about new algorithms in terms of these three parts can demystify how they operate and highlight their key differences.
Hypothesis Space (The Model Family): This is the set of all possible models the algorithm is allowed to consider. For example, in linear regression, the hypothesis space is the set of all possible straight lines. For a decision tree, it’s the set of all possible branching rules. The choice of hypothesis space imposes a certain structure or bias on the solution.
Objective Function (The Goal): This function defines what a “good” model looks like. It measures how well a particular model from the hypothesis space fits the training data. For instance, in regression, a common objective function is the Mean Squared Error (MSE), which penalizes models for making large prediction errors. The goal of learning is to find the model that minimizes this objective function.
Learning Algorithm (The Optimizer): This is the computational procedure used to search through the hypothesis space and find the model that best minimizes the objective function. This could be a straightforward mathematical formula (as in simple linear regression) or a complex iterative process (as in training neural networks).
By framing algorithms in this way, we can see, for example, that Ridge and Lasso regression share the same hypothesis space and learning algorithm as linear regression but differ in their objective function, which includes a penalty for complexity. This small change in the objective function has profound effects on the final model, helping to prevent overfitting.
20.2 Supervised Learning
20.2.1 Linear regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is called simple linear regression; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.
In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution of the response given the values of the predictors, rather than on the joint probability distribution of all of these variables, which is the domain of multivariate analysis.
Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.
20.2.2 K-nearest Neighbor
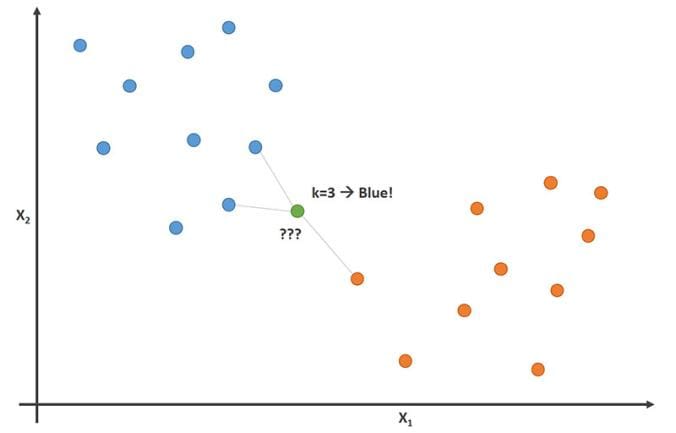
The k-nearest neighbors algorithm (k-NN) is a non-parametric supervised learning method first developed by Evelyn Fix and Joseph Hodges in 1951, and later expanded by Thomas Cover. It is used for classification and regression. In both cases, the input consists of the k closest training examples in a data set.
The k-nearest neighbor (k-NN) algorithm is a simple, yet powerful, supervised machine learning method used for classification and regression tasks. It is an instance-based, non-parametric learning method that stores the entire training dataset and makes predictions based on the similarity between data points. The underlying principle of the k-NN algorithm is that similar data points (those that are close to each other in multidimensional space) are likely to have similar outcomes or belong to the same class.
Here’s a description of how the k-NN algorithm works:
- Determine the value of k: The first step is to choose the number of nearest neighbors (k) to consider when making predictions. The value of k is a user-defined hyperparameter and can significantly impact the algorithm’s performance. A small value of k can lead to overfitting, while a large value may result in underfitting.
- Compute distance: Calculate the distance between the new data point (query point) and each data point in the training dataset. The most common distance metrics used are Euclidean, Manhattan, and Minkowski distance. The choice of distance metric depends on the problem and the nature of the data.
- Find k-nearest neighbors: Identify the k data points in the training dataset that are closest to the query point, based on the chosen distance metric.
- Make predictions: Once the k-nearest neighbors are identified, the final step is to make predictions. The prediction for the query point can be made in two ways:
- For classification, determine the class labels of the k-nearest neighbors and assign the class label with the highest frequency (majority vote) to the query point. In case of a tie, one can choose the class with the smallest average distance to the query point or randomly select one among the tied classes.
- For regression tasks, the k-NN algorithm follows a similar process, but instead of majority voting, it calculates the mean (or median) of the target values of the k-nearest neighbors and assigns it as the prediction for the query point.
The k-NN algorithm is known for its simplicity, ease of implementation, and ability to handle multi-class problems. However, it has some drawbacks, such as high computational cost (especially for large datasets), sensitivity to the choice of k and distance metric, and poor performance with high-dimensional or noisy data. Scaling and preprocessing the data, as well as using dimensionality reduction techniques, can help mitigate some of these issues.
In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor.
In k-NN regression, the output is the property value for the object. This value is the average of the values of k nearest neighbors.
k-NN is a type of classification where the function is only approximated locally and all computation is deferred until function evaluation. Since this algorithm relies on distance for classification, if the features represent different physical units or come in vastly different scales then normalizing the training data can improve its accuracy dramatically.
Both for classification and regression, a useful technique can be to assign weights to the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. For example, a common weighting scheme consists in giving each neighbor a weight of 1/d, where d is the distance to the neighbor.
The neighbors are taken from a set of objects for which the class (for k-NN classification) or the object property value (for k-NN regression) is known. This can be thought of as the training set for the algorithm, though no explicit training step is required.
20.3 Penalized regression
Adapted from http://www.sthda.com/english/articles/37-model-selection-essentials-in-r/153-penalized-regression-essentials-ridge-lasso-elastic-net/.
Penalized regression is a type of regression analysis that introduces a penalty term to the loss function in order to prevent overfitting and improve the model’s ability to generalize. Remember that in regression, the loss function is the sum of squares Equation 20.1.
\[L = \sum_{i=0}^{n}{(\hat{y}_i - y_i)}^2 \tag{20.1}\]
In Equation 20.1, \(\hat{y}_i\) is the predicted output, \(y_i\) is the actual output, and n is the number of observations. The goal of regression is to minimize the loss function by finding the optimal values of the model parameters or coefficients. The model parameters are estimated using the training data. The model is then evaluated using the test data. If the model performs well on the training data but poorly on the test data, it is said to be overfit. Overfitting occurs when the model learns the training data too well, including the noise, and is not able to generalize well to new data. This is a common problem in machine learning, particularly when there are a large number of predictors compared to the number of observations, and can be addressed by penalized regression.
The two most common types of penalized regression are Ridge Regression (L2 penalty) and LASSO Regression (L1 penalty). Both Ridge and LASSO help to reduce model complexity and prevent over-fitting which may result from simple linear regression. However, the choice between Ridge and LASSO depends on the situation and the dataset at hand. If feature selection is important for the interpretation of the model, LASSO might be preferred. If the goal is prediction accuracy and the model needs to retain all features, Ridge might be the better choice.
20.3.1 Ridge regression
Ridge regression shrinks the regression coefficients, so that variables, with minor contribution to the outcome, have their coefficients close to zero. The shrinkage of the coefficients is achieved by penalizing the regression model with a penalty term called L2-norm, which is the sum of the squared coefficients. The amount of the penalty can be fine-tuned using a constant called lambda (λ). Selecting a good value for λ is critical. When λ=0, the penalty term has no effect, and ridge regression will produce the classical least square coefficients. However, as λ increases to infinite, the impact of the shrinkage penalty grows, and the ridge regression coefficients will get close zero. The loss function for Ridge Regression is:
\[L = \sum_{i=0}^{n}{(\hat{y}_i - y_i)}^2 + \lambda\sum_{j=0}^{k} \beta_j^2 \tag{20.2}\]
Here, \(\hat{y}_i\) is the predicted output, \(y_i\) is the actual output, \({\beta_j}\) represents the model parameters or coefficients, and λ is the regularization parameter. The second term, λ∑βj^2, is the penalty term where all parameters are squared and summed. Ridge regression tends to shrink the coefficients but doesn’t necessarily zero them.
Note that, in contrast to the ordinary least square regression, ridge regression is highly affected by the scale of the predictors. Therefore, it is better to standardize (i.e., scale) the predictors before applying the ridge regression (James et al. 2014), so that all the predictors are on the same scale. The standardization of a predictor x, can be achieved using the formula \(x' = \frac{x}{sd(x)}\), where \(sd(x)\) is the standard deviation of \(x\). The consequence of this is that, all standardized predictors will have a standard deviation of one allowing the final fit to not depend on the scale on which the predictors are measured.
One important advantage of the ridge regression, is that it still performs well, compared to the ordinary least square method (see Equation 20.1), in a situation where you have a large multivariate data with the number of predictors (p) larger than the number of observations (n). One disadvantage of the ridge regression is that, it will include all the predictors in the final model, unlike the stepwise regression methods, which will generally select models that involve a reduced set of variables. Ridge regression shrinks the coefficients towards zero, but it will not set any of them exactly to zero. The LASSO regression is an alternative that overcomes this drawback.
20.3.2 LASSO regression
LASSO stands for Least Absolute Shrinkage and Selection Operator. It shrinks the regression coefficients toward zero by penalizing the regression model with a penalty term called L1-norm, which is the sum of the absolute coefficients. In the case of LASSO regression, the penalty has the effect of forcing some of the coefficient estimates, with a minor contribution to the model, to be exactly equal to zero. This means that, LASSO can be also seen as an alternative to the subset selection methods for performing variable selection in order to reduce the complexity of the model. As in ridge regression, selecting a good value of \(\lambda\) for the LASSO is critical. The loss function for LASSO Regression is:
\[L = \sum_{i=0}^{n}{(\hat{y}_i - y_i)}^2 + \lambda\sum_{j=0}^{k} |\beta_j| \tag{20.3}\]
Similar to Ridge, ŷi is the predicted output, yi is the actual output, βj represents the model parameters or coefficients, and λ is the regularization parameter. The second term, λ∑|βj|, is the penalty term where the absolute values of all parameters are summed. LASSO regression tends to shrink the coefficients and can zero out some of them, effectively performing variable selection.
One obvious advantage of LASSO regression over ridge regression, is that it produces simpler and more interpretable models that incorporate only a reduced set of the predictors. However, neither ridge regression nor the LASSO will universally dominate the other. Generally, LASSO might perform better in a situation where some of the predictors have large coefficients, and the remaining predictors have very small coefficients. Ridge regression will perform better when the outcome is a function of many predictors, all with coefficients of roughly equal size (James et al. 2014).
Cross-validation methods can be used for identifying which of these two techniques is better on a particular data set.
20.3.3 Elastic Net
Elastic Net produces a regression model that is penalized with both the L1-norm and L2-norm. The consequence of this is to effectively shrink coefficients (like in ridge regression) and to set some coefficients to zero (as in LASSO).
20.3.4 Classification and Regression Trees (CART)
Decision Tree Learning is supervised learning approach used in statistics, data mining and machine learning. In this formalism, a classification or regression decision tree is used as a predictive model to draw conclusions about a set of observations. Decision trees are a popular machine learning method used for both classification and regression tasks. They are hierarchical, tree-like structures that model the relationship between features and the target variable by recursively splitting the data into subsets based on the feature values. Each internal node in the tree represents a decision or test on a feature, and each branch represents the outcome of that test. The leaf nodes contain the final prediction, which is the majority class for classification tasks or the mean/median of the target values for regression tasks.
Here’s an overview of the decision tree learning process:
- Select the best feature and split value: Start at the root node and choose the feature and split value that results in the maximum reduction of impurity (or increase in information gain) in the child nodes. For classification tasks, impurity measures like Gini index or entropy are commonly used, while for regression tasks, mean squared error (MSE) or mean absolute error (MAE) can be used.
- Split the data: Partition the dataset into subsets based on the chosen feature and split value.
- Recursion: Repeat steps 1 and 2 for each subset until a stopping criterion is met. Stopping criteria can include reaching a maximum tree depth, a minimum number of samples per leaf, or no further improvement in impurity.
- Prune the tree (optional): To reduce overfitting, decision trees can be pruned by removing branches that do not significantly improve the model’s performance on the validation dataset. This can be done using techniques like reduced error pruning or cost-complexity pruning.
Decision trees have several advantages, such as:
- Interpretability
- They are easy to understand, visualize, and explain, even for non-experts.
- Minimal data preprocessing
- Decision trees can handle both numerical and categorical data, and they are robust to outliers and missing values.
- Non-linear relationships
- They can capture complex non-linear relationships between features and the target variable.
However, decision trees also have some drawbacks:
- Overfitting
- They are prone to overfitting, especially when the tree is deep or has few samples per leaf. Pruning and setting stopping criteria can help mitigate this issue.
- Instability
- Small changes in the data can lead to different tree structures. This can be addressed by using ensemble methods like random forests or gradient boosting machines (GBMs).
- Greedy learning
- Decision tree algorithms use a greedy approach, meaning they make locally optimal choices at each node. This may not always result in a globally optimal tree.
Despite these limitations, decision trees are widely used in various applications due to their simplicity, interpretability, and ability to handle diverse data types.
20.3.5 RandomForest
Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the mean or average prediction of the individual trees is returned. Random decision forests correct for decision trees’ habit of overfitting to their training set. Random forests generally outperform decision trees, but their accuracy is lower than gradient boosted trees[citation needed]. However, data characteristics can affect their performance.
The first algorithm for random decision forests was created in 1995 by Tin Kam Ho using the random subspace method, which, in Ho’s formulation, is a way to implement the “stochastic discrimination” approach to classification proposed by Eugene Kleinberg.
An extension of the algorithm was developed by Leo Breiman and Adele Cutler, who registered “Random Forests” as a trademark in 2006 (as of 2019[update], owned by Minitab, Inc.). The extension combines Breiman’s “bagging” idea and random selection of features, introduced first by Ho and later independently by Amit and Geman in order to construct a collection of decision trees with controlled variance.
Random forests are frequently used as “blackbox” models in businesses, as they generate reasonable predictions across a wide range of data while requiring little configuration.