8 Matrices

Author

Affiliation

University of Colorado
Anschutz School of Medicine

Published

June 1, 2024

Modified

June 4, 2025

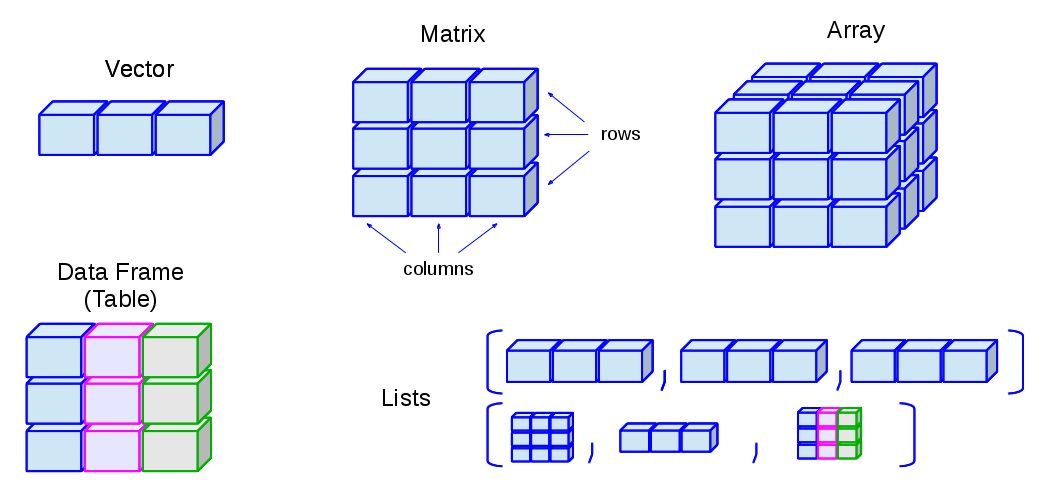
A matrix is a rectangular collection of the same data type (see Figure 8.1). It can be viewed as a collection of column vectors all of the same length and the same type (i.e. numeric, character or logical) OR a collection of row vectors, again all of the same type and length. A data.frame is also a rectangular array. All of the columns must be the same length, but they may be of different types. The rows and columns of a matrix or data frame can be given names. However these are implemented differently in R; many operations will work for one but not both, often a source of confusion.

Figure 8.1: A matrix is a collection of column vectors.

8.1 Creating a matrix

There are many ways to create a matrix in R. One of the simplest is to use the matrix() function. In the code below, we’ll create a matrix from a vector from 1:16.

mat1 <- matrix(1:16,nrow=4)
mat1

     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

The same is possible, but specifying that the matrix be “filled” by row.

mat1 <- matrix(1:16,nrow=4,byrow = TRUE)
mat1

     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12
[4,]   13   14   15   16

Notice the subtle difference in the order that the numbers go into the matrix.

We can also build a matrix from parts by “binding” vectors together:

x <- 1:10 
y <- rnorm(10)

Each of the vectors above is of length 10 and both are “numeric”, so we can make them into a matrix. Using rbind binds rows (r) into a matrix.

mat <- rbind(x,y)
mat

       [,1]        [,2]     [,3]       [,4]       [,5]      [,6]      [,7]
x  1.000000  2.00000000 3.000000  4.0000000  5.0000000  6.000000  7.000000
y -1.151193 -0.09401175 1.016198 -0.1788507 -0.9842443 -1.214426 -1.089794
      [,8]       [,9]      [,10]
x  8.00000  9.0000000 10.0000000
y -2.23542 -0.4612952  0.4178649

The alternative to rbind is cbind that binds columns (c) together.

mat <- cbind(x,y)
mat

       x           y
 [1,]  1 -1.15119280
 [2,]  2 -0.09401175
 [3,]  3  1.01619820
 [4,]  4 -0.17885066
 [5,]  5 -0.98424426
 [6,]  6 -1.21442596
 [7,]  7 -1.08979410
 [8,]  8 -2.23542017
 [9,]  9 -0.46129523
[10,] 10  0.41786492

Inspecting the names associated with rows and columns is often useful, particularly if the names have human meaning.

rownames(mat)

NULL

colnames(mat)

[1] "x" "y"

We can also change the names of the matrix by assigning valid names to the columns or rows.

colnames(mat) = c('apples','oranges')
colnames(mat)

[1] "apples"  "oranges"

mat

      apples     oranges
 [1,]      1 -1.15119280
 [2,]      2 -0.09401175
 [3,]      3  1.01619820
 [4,]      4 -0.17885066
 [5,]      5 -0.98424426
 [6,]      6 -1.21442596
 [7,]      7 -1.08979410
 [8,]      8 -2.23542017
 [9,]      9 -0.46129523
[10,]     10  0.41786492

Matrices have dimensions.

dim(mat)

[1] 10  2

nrow(mat)

[1] 10

ncol(mat)

[1] 2

8.2 Accessing elements of a matrix

Indexing for matrices works as for vectors except that we now need to include both the row and column (in that order). We can access elements of a matrix using the square bracket [ indexing method. Elements can be accessed as var[r, c]. Here, r and c are vectors describing the elements of the matrix to select.

Important

The indices in R start with one, meaning that the first element of a vector or the first row/column of a matrix is indexed as one.

This is different from some other programming languages, such as Python, which use zero-based indexing, meaning that the first element of a vector or the first row/column of a matrix is indexed as zero.

It is important to be aware of this difference when working with data in R, especially if you are coming from a programming background that uses zero-based indexing. Using the wrong index can lead to unexpected results or errors in your code.

# The 2nd element of the 1st row of mat
mat[1,2]

  oranges 
-1.151193

# The first ROW of mat
mat[1,]

   apples   oranges 
 1.000000 -1.151193

# The first COLUMN of mat
mat[,1]

 [1]  1  2  3  4  5  6  7  8  9 10

# and all elements of mat that are > 4; note no comma
mat[mat>4]

[1]  5  6  7  8  9 10

## [1]  5  6  7  8  9 10

Caution

Note that in the last case, there is no “,”, so R treats the matrix as a long vector (length=20). This is convenient, sometimes, but it can also be a source of error, as some code may “work” but be doing something unexpected.

We can also use indexing to exclude a row or column by prefixing the selection with a - sign.

mat[,-1]       # remove first column

 [1] -1.15119280 -0.09401175  1.01619820 -0.17885066 -0.98424426 -1.21442596
 [7] -1.08979410 -2.23542017 -0.46129523  0.41786492

mat[-c(1:5),]  # remove first five rows

     apples    oranges
[1,]      6 -1.2144260
[2,]      7 -1.0897941
[3,]      8 -2.2354202
[4,]      9 -0.4612952
[5,]     10  0.4178649

8.3 Changing values in a matrix

We can create a matrix filled with random values drawn from a normal distribution for our work below.

m = matrix(rnorm(20),nrow=10)
summary(m)

       V1                V2         
 Min.   :-1.8330   Min.   :-2.0497  
 1st Qu.:-0.7606   1st Qu.:-0.4389  
 Median : 0.7864   Median : 0.6033  
 Mean   : 0.2856   Mean   : 0.6738  
 3rd Qu.: 0.9019   3rd Qu.: 1.7985  
 Max.   : 2.3502   Max.   : 2.9927

Multiplication and division works similarly to vectors. When multiplying by a vector, for example, the values of the vector are reused. In the simplest case, let’s multiply the matrix by a constant (vector of length 1).

# multiply all values in the matrix by 20
m2 = m*20
summary(m2)

       V1                V2         
 Min.   :-36.661   Min.   :-40.994  
 1st Qu.:-15.211   1st Qu.: -8.779  
 Median : 15.729   Median : 12.065  
 Mean   :  5.711   Mean   : 13.475  
 3rd Qu.: 18.038   3rd Qu.: 35.969  
 Max.   : 47.004   Max.   : 59.854

By combining subsetting with assignment, we can make changes to just part of a matrix.

# and add 100 to the first column of m
m2[,1] = m2[,1] + 100
# summarize m
summary(m2)

       V1               V2         
 Min.   : 63.34   Min.   :-40.994  
 1st Qu.: 84.79   1st Qu.: -8.779  
 Median :115.73   Median : 12.065  
 Mean   :105.71   Mean   : 13.475  
 3rd Qu.:118.04   3rd Qu.: 35.969  
 Max.   :147.00   Max.   : 59.854

A somewhat common transformation for a matrix is to transpose which changes rows to columns. One might need to do this if an assay output from a lab machine puts samples in rows and genes in columns, for example, while in Bioconductor/R, we often want the samples in columns and the genes in rows.

t(m2)

          [,1]       [,2]      [,3]      [,4]      [,5]      [,6]       [,7]
[1,] 116.89722 147.004355 116.19088  99.50672 121.81061  63.33906 118.417923
[2,]  59.85408  -9.877637  12.99534 -40.99377  51.33027 -11.52863  -5.482144
         [,8]      [,9]    [,10]
[1,] 78.79549 115.26654 79.88263
[2,] 11.13558  29.04172 38.27873

8.4 Calculations on matrix rows and columns

Again, we just need a matrix to play with. We’ll use rnorm again, but with a slight twist.

m3 = matrix(rnorm(100,5,2),ncol=10) # what does the 5 mean here? And the 2?

Since these data are from a normal distribution, we can look at a row (or column) to see what the mean and standard deviation are.

mean(m3[,1])

[1] 6.709692

sd(m3[,1])

[1] 1.425251

# or a row
mean(m3[1,])

[1] 4.86667

sd(m3[1,])

[1] 2.102434

There are some useful convenience functions for computing means and sums of data in all of the columns and rows of matrices.

colMeans(m3)

 [1] 6.709692 4.968957 5.961377 4.572742 5.293570 4.130627 4.195079 4.475901
 [9] 5.076318 5.360578

rowMeans(m3)

 [1] 4.866670 4.100055 4.814678 5.800869 5.813489 5.485770 4.889247 5.444376
 [9] 4.603745 4.925941

rowSums(m3)

 [1] 48.66670 41.00055 48.14678 58.00869 58.13489 54.85770 48.89247 54.44376
 [9] 46.03745 49.25941

colSums(m3)

 [1] 67.09692 49.68957 59.61377 45.72742 52.93570 41.30627 41.95079 44.75901
 [9] 50.76318 53.60578

We can look at the distribution of column means:

# save as a variable
cmeans = colMeans(m3)
summary(cmeans)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  4.131   4.500   5.023   5.074   5.344   6.710

Note that this is centered pretty closely around the selected mean of 5 above.

How about the standard deviation? There is not a colSd function, but it turns out that we can easily apply functions that take vectors as input, like sd and “apply” them across either the rows (the first dimension) or columns (the second) dimension.

csds = apply(m3, 2, sd)
summary(csds)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.7965  1.8319  2.0329  1.8965  2.1867  2.3309

Again, take a look at the distribution which is centered quite close to the selected standard deviation when we created our matrix.

8.5 Exercises

8.5.1 Data preparation

For this set of exercises, we are going to rely on a dataset that comes with R. It gives the number of sunspots per month from 1749-1983. The dataset comes as a ts or time series data type which I convert to a matrix using the following code.

Just run the code as is and focus on the rest of the exercises.

data(sunspots)
sunspot_mat <- matrix(as.vector(sunspots),ncol=12,byrow = TRUE)
colnames(sunspot_mat) <- as.character(1:12)
rownames(sunspot_mat) <- as.character(1749:1983)

8.5.2 Questions

After the conversion above, what does sunspot_mat look like? Use functions to find the number of rows, the number of columns, the class, and some basic summary statistics.
Show answer
```
ncol(sunspot_mat)
nrow(sunspot_mat)
dim(sunspot_mat)
summary(sunspot_mat)
head(sunspot_mat)
tail(sunspot_mat)
```
Practice subsetting the matrix a bit by selecting:
- The first 10 years (rows)
- The month of July (7th column)
- The value for July, 1979 using the rowname to do the selection.
Show answer
```
sunspot_mat[1:10,]
sunspot_mat[,7]
sunspot_mat['1979',7]
```

These next few exercises take advantage of the fact that calling a univariate statistical function (one that expects a vector) works for matrices by just making a vector of all the values in the matrix. What is the highest (max) number of sunspots recorded in these data?
Show answer
```
max(sunspot_mat)
```
And the minimum?
Show answer
```
min(sunspot_mat)
```
And the overall mean and median?
Show answer
```
mean(sunspot_mat)
median(sunspot_mat)
```
Use the hist() function to look at the distribution of all the monthly sunspot data.
Show answer
```
hist(sunspot_mat)
```
Read about the breaks argument to hist() to try to increase the number of breaks in the histogram to increase the resolution slightly. Adjust your hist() and breaks to your liking.
Show answer
```
hist(sunspot_mat, breaks=40)
```
Now, let’s move on to summarizing the data a bit to learn about the pattern of sunspots varies by month or by year. Examine the dataset again. What do the columns represent? And the rows?
Show answer
```
# just a quick glimpse of the data will give us a sense
head(sunspot_mat)
```

We’d like to look at the distribution of sunspots by month. How can we do that?

Show answer

# the mean of the columns is the mean number of sunspots per month.
colMeans(sunspot_mat)

# Another way to write the same thing:
apply(sunspot_mat, 2, mean)

Assign the month summary above to a variable and summarize it to get a sense of the spread over months.
Show answer
```
monthmeans = colMeans(sunspot_mat)
summary(monthmeans)
```
Play the same game for years to get the per-year mean?
Show answer
```
ymeans = rowMeans(sunspot_mat)
summary(ymeans)
```
Make a plot of the yearly means. Do you see a pattern?
Show answer
```
plot(ymeans)
# or make it clearer
plot(ymeans, type='l')
```