Estimate R(t) from cumulative case time series

Source: R/estimate_Rt.R

Given a case-tracking dataset, determine the basic reproduction index over time.

estimate_Rt(
  df,
  filter_expression,
  cases_column = "count",
  date_column = "date",
  method,
  config,
  cumulative = TRUE,
  estimation_family = "epiestim",
  invert = FALSE,
  quiet = TRUE,
  ...
)

Arguments

df

a data.frame containing at least a date column and a cases column, describing the cumulative cases at each date. Note that dates MUST NOT REPEAT and the function will check that this is the case. Use the filter_expression parameter to limit the data.frame to achieve non-duplicated dates from the typical case-tracking datasets in sars2pack.

filter_expression

a dplyr::filter expression, applied directly to the data.frame prior to calculating Rt. This is a useful way to write a one-liner from any of the case-tracking datasets.

cases_column

character(1) name of (cumulative) cases column in the input data.frame

date_column

character(1) name of date column in the input data.frame

method

character(1) passed to EpiEstim::estimate_R()

config

list() passed to EpiEstim::make_config(). Typically used to set up the serial interval distribution.

cumulative

logical(1) whether the case counts are cumulative (TRUE) or are daily incidence (FALSE)

estimation_family

One of epiestim

invert

Unused default FALSE, but if TRUE, returns 1/R(t) or related estimate, useful for plotting, since we are often most interested in looking at R(t) near or below 1.

quiet

logical(1) whether or not to provide messages, etc.

...

passed to the estimation method

Value

For the epiestim method, returns a data.frame with columns: - Mean(R) - Std(R) - Quantile.0.025(R) - Quantile.0.05(R) - Quantile.0.25(R) - Median(R) - Quantile.0.75(R) - Quantile.0.95(R) - Quantile.0.975(R)" - date_start - date_end

Examples

nyt = nytimes_state_data()
head(nyt)
#> # A tibble: 6 × 5
#>   date       state      fips  count subset   
#>   <date>     <chr>      <chr> <dbl> <chr>    
#> 1 2020-01-21 Washington 00053     1 confirmed
#> 2 2020-01-22 Washington 00053     1 confirmed
#> 3 2020-01-23 Washington 00053     1 confirmed
#> 4 2020-01-24 Illinois   00017     1 confirmed
#> 5 2020-01-24 Washington 00053     1 confirmed
#> 6 2020-01-25 California 00006     1 confirmed

nystate_Rt = estimate_Rt(
    nyt,
    filter_expression = state=='New York' & subset=='confirmed',
    estimation_family='epiestim',
    cumulative=TRUE,
    method = 'parametric_si',
    config = list(mean_si=3.96, std_si=4.75))
head(nystate_Rt)
#>   t_start t_end  Mean(R)    Std(R) Quantile.0.025(R) Quantile.0.05(R)
#> 1       2     8 2.428545 0.2358812          1.988294         2.054010
#> 2       3     9 2.272241 0.1906823          1.913890         1.967954
#> 3       4    10 1.998458 0.1523810          1.710949         1.754590
#> 4       5    11 1.865457 0.1296582          1.619972         1.657433
#> 5       6    12 2.204895 0.1262519          1.964362         2.001419
#> 6       7    13 1.987600 0.1022311          1.792256         1.822487
#>   Quantile.0.25(R) Median(R) Quantile.0.75(R) Quantile.0.95(R)
#> 1         2.265560  2.420913         2.583212         2.829117
#> 2         2.140887  2.266910         2.397784         2.594716
#> 3         1.893677  1.994586         2.099018         2.255532
#> 4         1.776444  1.862454         1.951197         2.083725
#> 5         2.118477  2.202486         2.288687         2.416589
#> 6         1.917724  1.985847         2.055565         2.158691
#>   Quantile.0.975(R) date_start   date_end
#> 1          2.912167 2020-03-02 2020-03-08
#> 2          2.660890 2020-03-03 2020-03-09
#> 3          2.307967 2020-03-04 2020-03-10
#> 4          2.128007 2020-03-05 2020-03-11
#> 5          2.459119 2020-03-06 2020-03-12
#> 6          2.192902 2020-03-07 2020-03-13

library(ggplot2)
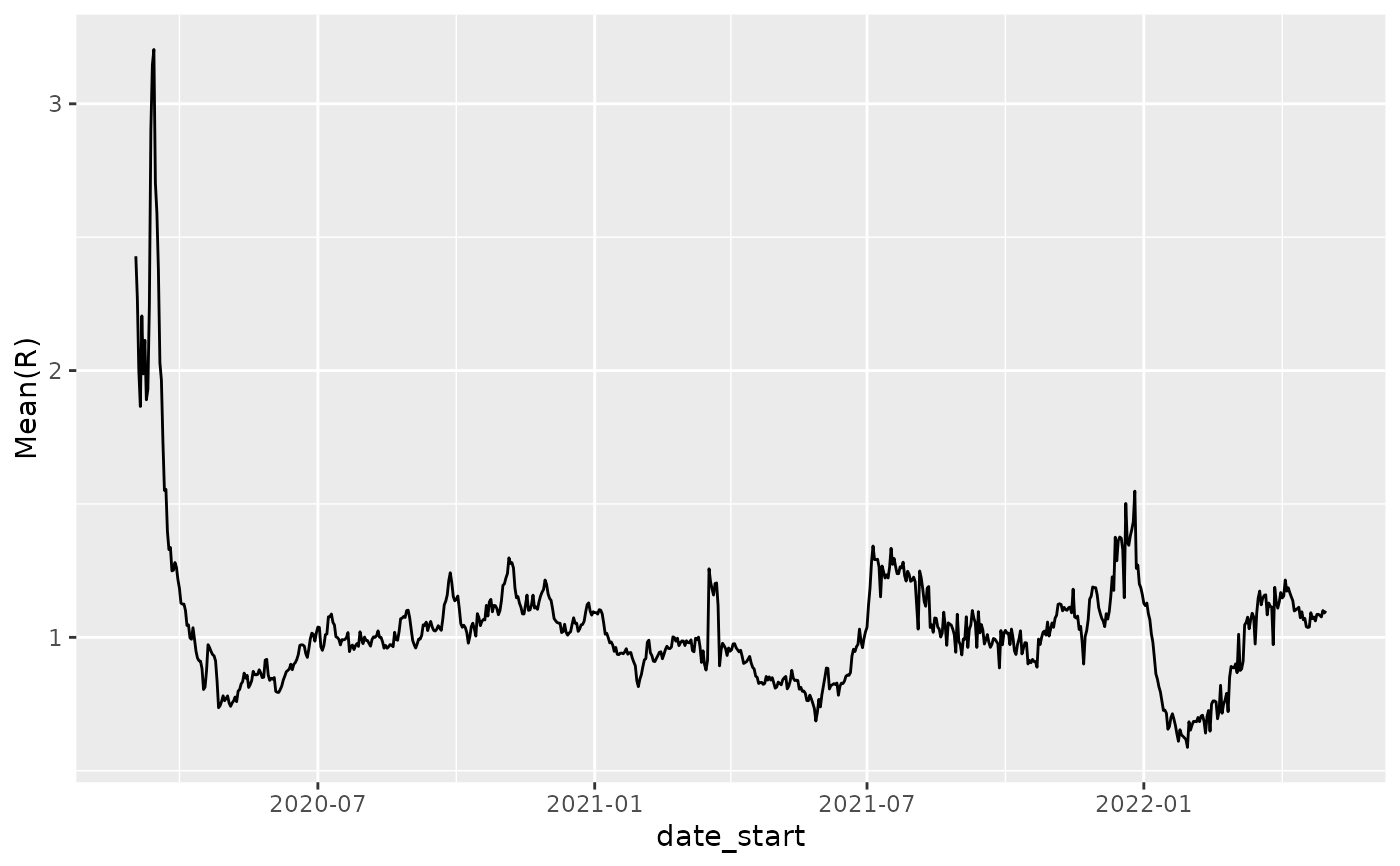
p = ggplot(nystate_Rt, aes(x=date_start,y=`Mean(R)`)) + geom_line()
p

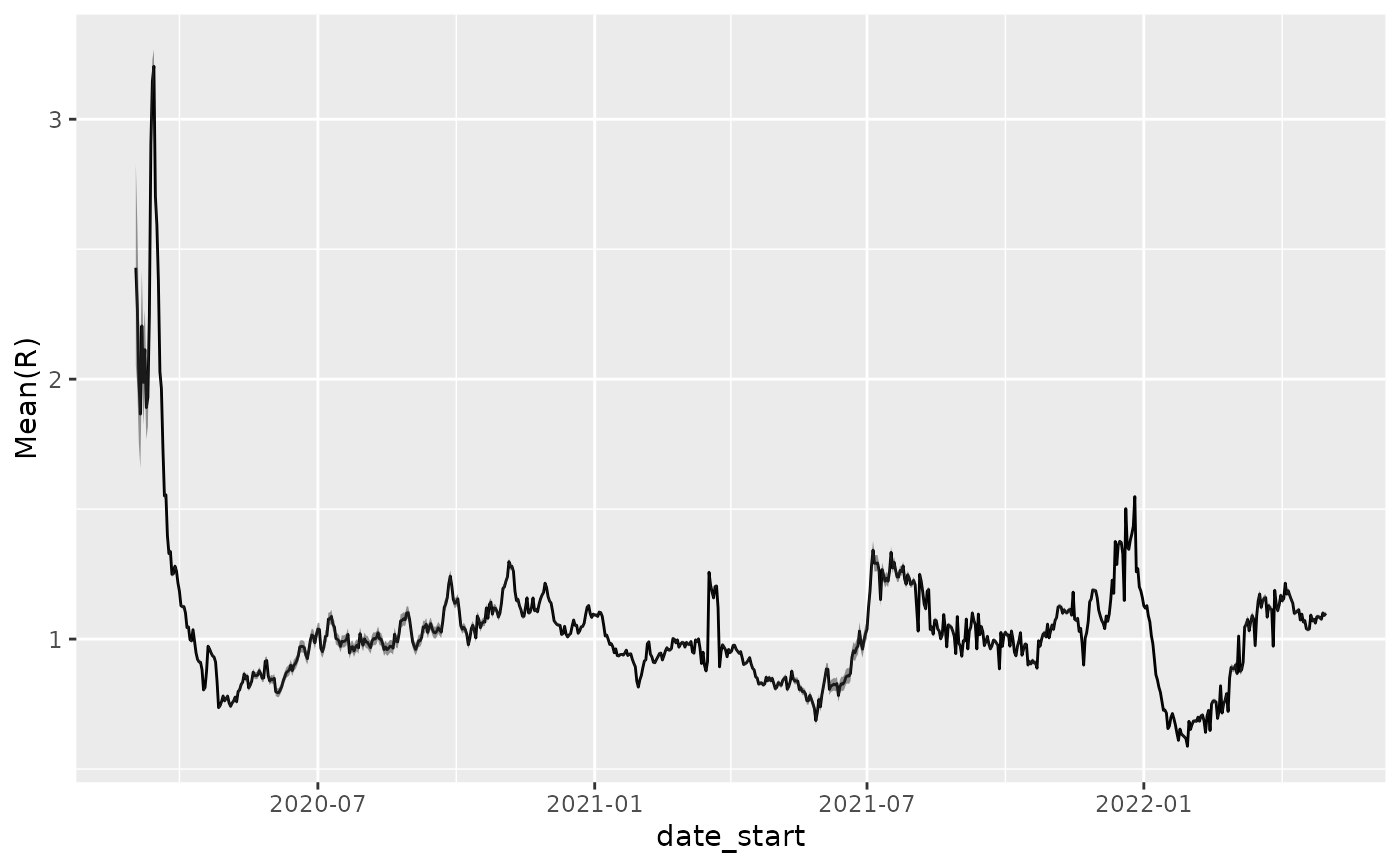
p + geom_ribbon(aes(ymin=`Quantile.0.05(R)`, ymax=`Quantile.0.95(R)`), alpha=0.5)


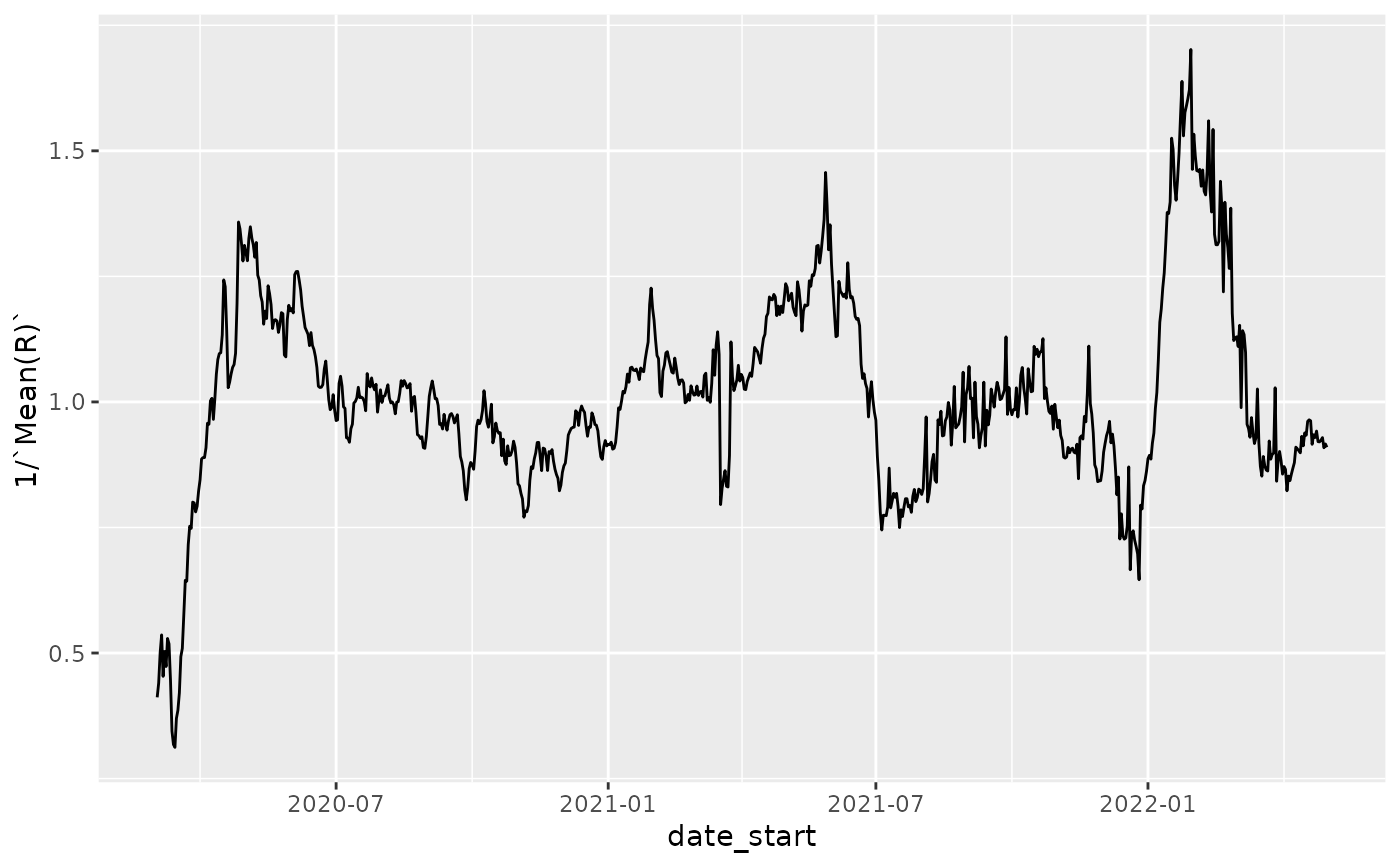
# plot 1/Rt to expand region around 1 since that is typically what
# is most interesting with respect to controls

p = ggplot(nystate_Rt, aes(x=date_start,y=1/`Mean(R)`)) + geom_line()
p

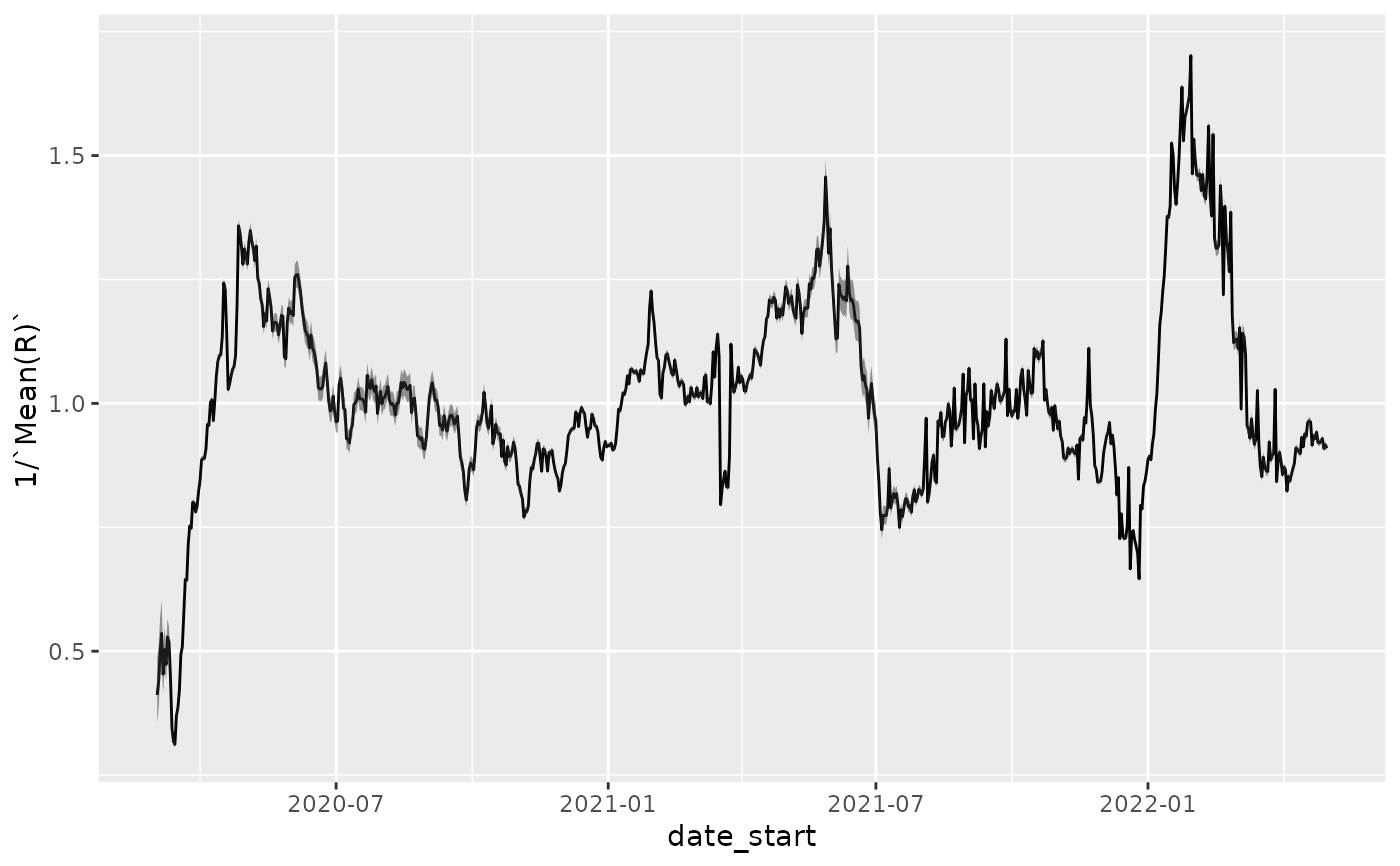
p + geom_ribbon(aes(ymax=1/`Quantile.0.05(R)`, ymin=1/`Quantile.0.95(R)`), alpha=0.5)


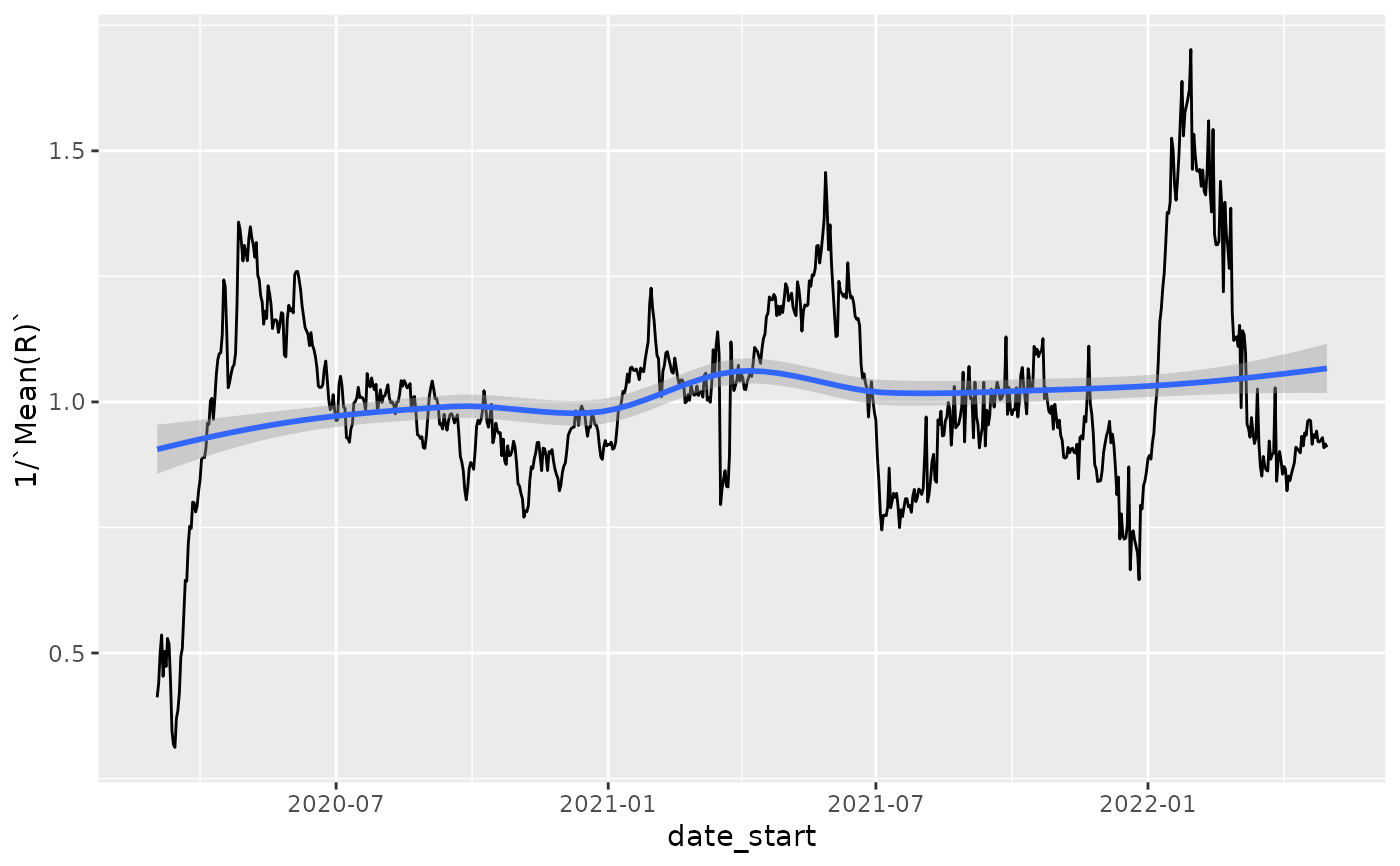
# and simple loess smoothing
p + geom_smooth()
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'



# super-cool use of tidyr, purrr, and dplyr to perform 
# calculations over all states:
if (FALSE) {
library(dplyr)
library(tidyr)
est_by = function(df) {
        estimate_Rt(
        df,
        estimation_family='epiestim',
        cumulative=TRUE,
        method = 'parametric_si',
        config = list(mean_si=3.96, std_si=4.75))
    }
z = nyt %>% dplyr::filter(subset=='confirmed') %>% tidyr::nest(-state) %>%
    dplyr::mutate(rt_df = purrr::map(data, est_by)) %>% tidyr::unnest(cols=rt_df)
p = ggplot(z,aes(x=date_start,y=1/`Mean(R)`, color=state)) + 
     ylim(c(0.5,1.25)) + 
     geom_smooth(se = FALSE)
p
library(plotly)
ggplotly(p)
}